Spiel 102 | Standardspiel | Xaver | Die Welt der Fraktale | Sieg der Werwölfe
-
- Standardspiel
-
Xaver -
23. Juni 2021 um 17:29
-
-
VOTE:MichaelCR97
-----------
Stand Tag 2
Jopnu (1): MichaelCR97
LB123 (1): Jopnu
MichaelCR97 (2): Lark, LB123
Verbleibende Zeit: 00:00:01
-
Wow LB
-
Ahh ich bin auch noch da
Lb sehr minimal
-
Erste Lynchung
Zitat von FayksSchaut was ich in den tiefen meiner Galerie gefunden habe: Fayks macht das Chaosspiel um Fraktale an regelmäßigen N-Ecken zu erzeugen für ihre Facharbeit. Natürlich schön per Hand weil meine Mathelehrerin mir das Programm nach dem ich mehrmals gefragt hab erst nach Abgabe gezeigt hat

20180316_121028.jpg
Falls sich jemand fragt, was Fayks da gemacht hat, praktischerweise hat Numberphile (bester YouTube-Kanal) ein Video zum Chaosspiel (das ich zufällig vor kurzem gesehen haben, und das mich auf die Idee gebracht hat, ein Spiel mit dem Thema Fraktale zu machen):
Externer Inhalt www.youtube.comInhalte von externen Seiten werden ohne Ihre Zustimmung nicht automatisch geladen und angezeigt.Durch die Aktivierung der externen Inhalte erklären Sie sich damit einverstanden, dass personenbezogene Daten an Drittplattformen übermittelt werden. Mehr Informationen dazu haben wir in unserer Datenschutzerklärung zur Verfügung gestellt.Aber kommen wir zu Fraktale in der Natur
Fraktale sind natürlich ideale mathematische Konstrukte mit einer unendlichen Detailtiefe. Da in der realen Welt Detailgenauigkeit leider durch Physik begrenzt ist, kann man so etwas nicht finden. Allerdings gibt es Annäherungen, die zumindest bis in eine gewisse Tiefe fraktale Muster aufweisen.
Wer das Video bis zum Ende geschaut hat, hat schon ein fraktales Objekt aus der Natur gesehen: Die gute alte Urzeitpflanze Farn, die man in jedem guten Wald finden kann.
Ich glaube, ich muss kein Bild von Farn posten. Eine mathematische Version des Farns ist das Barnsley Farn (benannt nach dem Mathematiker Michael Barnsley). Wie man gut erkennen kann, ähnelt jedes Teil des Farns dem gesamten Farn:

Generieren kann man das Barnsley Farn mittels sogenannten Iterierten Funktionensystemen (IFS), aber das zu erklären würde etwas zu mathematisch werden.
Kommen wir so dem Problem der Küstenlinien. Aus irgendeinem Grund interessieren sich Menschen für die Länge von Künsten. Neben so Fragen, wie ob man während Flut oder Ebbe misst, stellt sich auch die Frage, wie genau man die Küsten ausmisst. Tut man es über Satellitenbilder mit Linien von einem Kilometer Länge oder misst man per Hand mit dem Zollstock? Und macht es überhaupt einen großen Unterschied?
Wie sich herausstellt ja, es macht einen Unterschied, denn je genauer man eine Küste misst, desto größer ist der Wert, den man bekommt.
Hier zum Beispiel die Küste Englands:
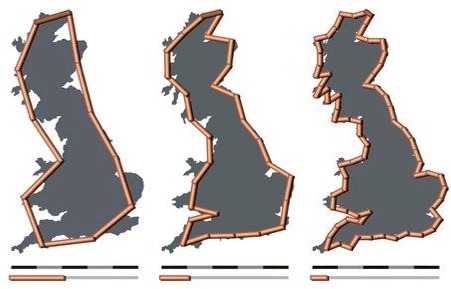
(Wikipedia hat dazu einen Eintrag mit dem wundervoll langen Titel How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension)
Der Grund: Küstenlinien sind fraktal. Und könnte man sie unendliche genau messen (was man leider nicht kann und außerdem besteht (soweit bekannt) alles aus Teilchen, die nicht unendlich klein sind), würde man feststellen, dass sie genauso wie z.B. die Koch-Kurve unendlich lang sind (wie bei der Koch-Kurve ist allerdings die durch sie begrenzte Fläche endlich).
Dabei sind nicht alle Küsten gleich fraktal. Während die Küste Großbritanniens eine fraktale Dimension von ca. 1,25* hat, ist die fraktale Dimension der Küste Norwegens mit all seinen Fjorden mit 1,52* wesentlich höher. Daher wenn man um einen festen Faktor genauer misst, wird die Küste Norwegens schneller größer als die Großbritanniens. Wenn ihr also nächstes Mal irgendwo Angaben der Länge einer Küste seht, nehmt sie mit einer großen Portion Skepsis, denn jede Küste ist in der Theorie unendlich lang.
*diese Werte wurden natürlich aus Messung berechnet
Kleiner Fun Fact: Die Tatsache, dass die Länge einer Küste von der Genauigkeit der Messung abhängt, wurde erst 1951 von Lewis Fry Richardson festgestellt, als er bemerkte, dass die Portugiesen die Länge ihrer Grenze zu Spanien mit 987 km angaben, die Spanier aber die Länge der Grenze zu Portugal mit 1214 km (die Portugiesen haben offensichtlich mit weniger großen Linien gemessen).
Dies sind nur zwei Beispiele für Fraktale in der Natur. Wenn man genau hinschaut, findet man sie überall: Bäume, Blätter, Romanesco, Schneeflocken, Wolken, Blitze, Flüsse, Berge, etc. sie alle haben fraktale Muster, die das Ganze im Kleinen wiederholen.
Stand Lynchung:Jopnu (1): MichaelCR97LB123 (1): JopnuMichaelCR97 (1): Lark(kommt schon Leute, ich weiß, dass ihr alle nicht viel zeit habt und das Spiel aufgrund seiner geringen Größe nicht viel Aktivität erzeugen kann, aber zwei Post pro Tag und eine Lynchstimme sind doch nicht zuviel verlangt?)Da Jopnu HD ist, entscheidet er, dass LB123 gelyncht wird. Er war *zensiert*. Jetzt ist er nur noch eine baumelnde Leiche.Stand Lynchung:
Jopnu (1): MichaelCR97
LB123 (1): Jopnu
MichaelCR97 (2): Lark, LB123
Ihr lyncht Michael, er war ein einfacher Dorfbewohner. Über den Sinn dieser Lynchung nachdenkend, geht ihr ins Bett.
Es wird Nacht
-----------
Stand Tag 2
Jopnu (1): MichaelCR97
LB123 (1): Jopnu
MichaelCR97 (2): Lark, LB123
Deadline abgelaufen
-
Xaver
25. Juni 2021 um 20:06 Hat den Titel des Themas von „Spiel 102 | Standardspiel | Xaver | Die Welt der Fraktale | 6/7“ zu „Spiel 102 | Standardspiel | Xaver | Die Welt der Fraktale | 5/7“ geändert. -
Zweite Nacht
Die Fraktale, die ich bislang präsentiert habe, sind vielleicht hübsch anzusehen, aber sie sind nicht besonders spannend. Egal, wie weit man in sie hineinzoomt, sieht man doch immer wieder nur dasselbe.
Anders sieht es bei dem nächsten Fraktal aus, der Mandelbrot-Menge.
Ich hoffe, ihr seid alle mit komplexen Zahlen vertraut, den wir betrachten nun die Folge zn über den komplexen Zahlen, wobei gilt:
z0 = 0
zn+1 = zn^2 + c
und das für jede komplexe Zahl c.
Die Folgen kann jetzt für verschiedene anhängig von c vier verschiedene Verhalten zeigen:
- gegen unendlichen divergieren (für z.B. c=1 ergibt 0, 0^2+1=1, 1^2+1=2, 2^2+1=5, 5^2+1=26, ...)
- gegen eine feste Zahl konvergieren (für c=-2 erhält man 0, -2, -2^2-2=2, 2^2-1=2, 2, 2, 2, 2, ...)
- zwischen mehreren Werten hin und her springen (c=-1 ergibt 0, -1, 0, -1, 0, -1, ...)
- chaotisches Verhalten (z.B. c=-1,5)
Genau dann, falls zn für c nicht divergiert, ist c in der Mandelbrot-Menge.
Diese unscheinbare Folge ergibt dieses komplexes Bild:

Die schwarzen Pixel sind, die zur Mandelbrot-Menge gehören, die restlichen Pixel kann man entsprechend der Schnelligkeit, mit der sie gegen Unendlich divergieren einfärben, um ein visuell ansprechenderes Bild zu erhalten:
Wenn man in die Mandelbrot-Menge reinzoomt, stellt man fest, dass man überall kleine nicht ganz identische Kopien von ihr (genannt Minibrote) findet. Hier z.B. in der Spitze, wo lauter Minibrote aufgereiht sind:

In dem Tal zwischen den beiden größten Teilen der Mandelbrot-Menge finden sich lauter stark verzerrte Minibrote:

Anmerkungen:
Die dünnen Filamente, die man auf den Bildern in verschieden Farben sieht, enthalten auch Teile der Mandelbrot-Menge, allerdings sind diese so dünn, dass sie auf den Bildern nur dadurch erkennbar sind, dass ihre Umgebung langsamer gegen Unendlich konvergiert.
Außerdem sind sämtliche Teile der Mandelbrot-Menge durch ebensolche Filamente miteinander verbunden, daher es gibt keine Inseln.
Je tiefer man in die Mandelbrot-Menge zoomt, desto mehr Details findet man und immer wieder wird man durch neue überrascht. Hier ein kleiner Zoom: https://upload.wikimedia.org/wikipedia/comm…equence_new.gif (nicht eingebettet, weil das Gif mit 23 MB etwas größer ist).
Hier ein paar von mir gemachte Schnappschüsse:





Falls wer selbst auf Entdeckungsreise gehen möchte, hier ein Tool, das ich selbst programmiert habe: http://xaver.byethost5.com/tools/mandelbrot4/
Sollte größtenteils selbsterklärend sein, aber falls wer Probleme hat, kann er mich ruhig fragen. Für tiefere Zooms, muss man übrigens die Anzahl an Iterationen immer höher stellen (wodurch es langsamer wird, die Bilder zu rendern).
Jemand hat die Umrisse der Mandelbrot-Menge riesengroß auf den Dorfplatz gezeichnet und in der Mitte liegt ... keine Leiche. Noch mal Glück gehabt, niemand wurde gefressen. Ob Fayks Mörder so sehr von den gefundenen Fraktalen fasziniert war(en), dass er/sie heute ganz vergessen hat/haben, nochmal zu morden? Ihr solltet vielleicht trotzdem versuchen heute jemand schuldiges zu finden und zu lynchen.
Es wird Tag Deadline auf 26.06.21 20:00 gesetzt
-
Lark könnte ich ins Dorf schieben. Muss ich mal sehen...
-
Oh nein Michael :o
Lark ist ein unschuldiger Engel. Dunno über die anderen.
-
Man shit....ich verpasse immer die Lynchung
Sry Michael

-
Keine Ahnung warum ihr Lark dafür dorfig habt
-
Als LB wohl dorf^^ bleiben Meemco oder Jopnu...
Hm
Fangen wir mal mit
VOTE:Jopnu an und schauen, was passsiert
-----------
Stand Tag 3
Jopnu (1): Lark
Verbleibende Zeit: 21:49:18
-
Alles anzeigen
Als LB wohl dorf^^ bleiben Meemco oder Jopnu...
Hm
Fangen wir mal mit
VOTE:Jopnu an und schauen, was passsiert
-----------
Stand Tag 3
Jopnu (1): Lark
Verbleibende Zeit: 21:49:18
Ähm was ist mit raphii?
Wenn du schon nach Ausschluss gehst
VOTE:LB123
-----------
Stand Tag 3
Jopnu (1): Lark
LB123 (1): Jopnu
Verbleibende Zeit: 21:28:47
-
Ähm was ist mit raphii?
+1
Als LB wohl dorf^^ bleiben Meemco oder Jopnu...
Warum eigentlich. Ich glaube ja an eine Dorf-Lark, aber du machst mir Angst...
-
Lb du hattest Michael vorgeworfen mit vielen Worten kaum Inhalt zu schreiben
Bei lark machst du es
Dorf aber Angst -> du hälst dir alles offen
Ärgerlich
-
Ich glaube mit Meemco fahren wir heute ganz gut
-
also sind sich schon drei von fünf sehr uneinig. klasse
-
Lb du hattest Michael vorgeworfen mit vielen Worten kaum Inhalt zu schreiben
das war eher wie er schrieb -> zu blumig zu viel Umschreibung ohne auf dem Punkt zu kommen
Dorf aber Angst -> du hälst dir alles offen
Ich halte sie für eine Dorf- Lark, habe aber trotzdem keine 100-prozent Sicherheit, wei ich sie nur schwer einschätzen kann.
-
Ich frage mich gerade übrigens, was ich von Jopnus Frage halten soll. Wenn ich klar Dorf-Lark sage, dann sollte fürr mich klar sein, dass cih sie schonf ür Dorf halte uch wenn mir die eine Situaion Angst gemacht hat.. Wenn cih mir alles offen halten wollte, hätte ich es weniger klar geschrieben
-
Als LB ich sag mal so, ich traue es dir als wolf nicht zu so random nach der Nacht mich ins Dorf zu stellen, deswegen bist du dorf
-
Zweite Lynchung
Ich war etwas beschäftigt (und vielleicht auch etwas faul), daher gibt es mehr Fraktale im Nachtpost.
In der Zwischenzeit bewundert die Lévy-C-Kurve:

Stand Lynchung:
Jopnu (1): Lark
LB123 (1): Jopnu
Da Jopnu HD ist, entscheidet er, dass LB123 gelyncht wird. Er war Heiler mit Ring des Lebens[1]. Jetzt ist er nur noch eine baumelnde Lévy-C-Kurve ähm ich meine Leiche.
Es wird Nacht
-----------
Stand Tag 3
Jopnu (1): Lark
LB123 (1): Jopnu
Deadline abgelaufen
Verlauf Tag 3
-
Xaver
26. Juni 2021 um 20:04 Hat den Titel des Themas von „Spiel 102 | Standardspiel | Xaver | Die Welt der Fraktale | 5/7“ zu „Spiel 102 | Standardspiel | Xaver | Die Welt der Fraktale | 4/7“ geändert. -

